Continuando a reprodução do artigo. No último texto que fiz a respeito, mostrei as regressões para identificar convergência absoluta e condicionada. Neste texto pretendo demonstrar como proceder para realizar os testes de identificação da dependência espacial nessas convergências.
Antes de continuar, vou deixar uma sequência de links para facilitar o acompanhamento do que está sendo feito.
Dissertação que originou o artigo, aqui;
Artigo publicado, aqui;
Resumo do que trata o artigo, aqui;
Reprodução das análises de convergência absoluta e condicionada,aqui.
Dependência espacial
Na prática, identificar se há dependência espacial significa identificar se há efeito estatisticamente significante do aspecto geográfico. Existem diferentes maneiras de fazer isso. Essas dependem do objeto que está sendo analisado e da metodologia utilizada. No artigo, o aspecto geográfico a ser analisado era a vizinhança de municípios nordestinos. Nesse sentido, o objetivo era saber se, além das variáveis inseridas nas regressões de convergência absoluta e condicionada, o desempenho econômico da vizinhança também teria algum impacto.
Para fazer essa análise, é necessário quantificar essa vizinhaça. Isso foi feito por meio matrizes de vizinhança. Essas matrizes são compostas de 1’s e 0’s (uns e zeros). Assim, a matriz é composta por linhas e colunas dos municípios nordestinos e, quando dois deles são vizinhos, a célula correspondente será 1, quando não, 0.
Tipos de Matrizes de Vizinhança
Para a construção dessas matrizes é necessário definir qual método será utilizado. Afinal, existem diferentes configurações de vizinhança possíveis. Nesse sentido, as composições analisadas no artigo foram as formações queen e root, de níveis 1 e 2. O que isso significa? As menções queen (rainha) e root (torre) remetem aos movimentos do xadrez e representam os vizinhos acima, abaixo e de cada lado, para o caso do root (como uma cruz). E os mesmos, mais os das diagonais, para o caso do formato queen (como um asterísco). Além disso, os diferentes níveis representam vizinhos de 1º grau e de 2º grau. Os de 2º grau são aqueles que, por exemplo, são vizinhos imediatos na mesma direação dos vizinhos imediatos (1º grau).Tudo isso, respeitando o formato da vizinhança, queen ou root.1
Parece confuso, mas, na verdade, é bastante simples.
Dados
Para construir essas matrizes de vizinhança é necessário ter o shapefile, o mapa dos municípios. Com base nesse mapa é que são criadas as matrizes de vizinhança. Para fazer isso, eu utilizei o software Geoda, que está disponível no link.
Acredito que seja possível fazer as mesmas matrizes no R, mas, como tive o trabalho de compor as Áreas Mínimas Comparáveis (AMC) e estou privilegiando a praticidade, não vou apresentar essa solução, pois não a conheço no momento. Para quem desejar se aventurar, o pacote a ser utilizado é o spdep, que tem manual e aplicações disponíveis aqui.
Aplicação
Inicialmente, temos que carregar os pacotes para a análise de dependência espacial (spdep), tabelas (stargazer) e gráficos (gplot2).
library(spdep)
library(stargazer)
library(ggplot2)
Feito isso, é necessário carregar a base de dados que estamos utilizando, a mesma dos outros textos.
BASE <- read.csv("http://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/NE1991.csv", header = T)
Leitura de dados
Agora, é necessário adicionar as matrizes de vizinhança à base de dados principal. Essas matrizes de defasagens espaciais serão relacionadas com os códigos dos municípios da base principal. No caso, criei quatro matrizes, pois ainda precisaremos testar qual é a mais adequada para este conjunto de municípios e período de análise.
Abaixo, a primeira função, read.gal faz a leitura da matriz. A segunda, nb2listw, faz a transformação de neighbor (nb) para uma lista de “pesos”, a matriz de vizinhança.
Q1<-read.gal("https://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/Q1.gal",BASE$MUN)
WQ1<-nb2listw(Q1)
Q2<-read.gal("https://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/Q2.gal",BASE$MUN)
WQ2<-nb2listw(Q2)
R1<-read.gal("https://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/R1.gal",BASE$MUN)
WR1<-nb2listw(R1)
R2<-read.gal("https://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/R2.gal",BASE$MUN)
WR2<-nb2listw(R2)
Teste I de Moran
O teste indicado para verificar se há dependência espacial no modelo econométrico é o I de Moran. O I de Moran faz um teste com base na relação do resíduo da regressão defasado espacialmente e dele sem essa defasagem. Tudo isso, normalizado pelo número de de observações e a soma de valores na matriz (bem resumidamente, para mais detalhes, veja na dissertação).
O teste, então, demanda a utilização das regressões. Para tanto, vamos refazer as regressões de convergência condicionada do último texto.
CC9110 <- lm(lng9110~lnProd1991+EMedio1991+Analf1991
+Urb1991+LnPop1991+Indus1991+Serv1991+Gini1991, data=BASE)
CC9100 <- lm(lng9100~lnProd1991+EMedio1991+Analf1991
+Urb1991+LnPop1991+Indus1991+Serv1991+Gini1991, data=BASE)
CC0010 <- lm(lng0010~lnProd2000+EMedio2000+Analf2000
+Urb2000+LnPop2000+Indus2000+Serv2000+Gini2000, data=BASE)
Os testes são feitos com a função lm.morantest. Para simplificar, só vou fazer aqui, os da regressão “CC9110” (Convergência Condicionada de 1991 a 2010), nas diferentes matrizes de ponderação:
Queen de grau 1: WQ1;
Queen de grau 2: WQ2;
Root de grau 1: WR1;
Root de grau 2: WR2
MQ19110<-lm.morantest(CC9110,WQ1)
MQ29110<-lm.morantest(CC9110,WQ2)
MR19110<-lm.morantest(CC9110,WR1)
MR29110<-lm.morantest(CC9110,WR2)
Os resultados podem ser vistos na tabela a seguir:
stargazer(cbind(MQ19110$estimate,MQ29110$estimate,
MR19110$estimate,MR29110$estimate),
type = "html",
title = "Resultados para o Teste I de Moran ",
align = T,
no.space = T
)
| Observed Moran I | 0.112 | 0.082 | 0.118 | 0.087 |
| Expectation | -0.002 | -0.002 | -0.002 | -0.002 |
| Variance | 0.0002 | 0.0001 | 0.0003 | 0.0001 |
Para facilitar a visualização, acabei suprimindo as estatísticas da tabela, mas acredite em mim, os I’s de Moran observados foram estatisticamente significantes. Isso significa que, se eles são estatísticamente diferentes de zero, há dependência espacial no modelo testado.
Também podemos analisar essa informação no gráfico. No caso do artigo, eu havia feito os gráficos pelo GeoDa. Também é possível gerar esse gráfico diretamente no R, com a função moran.plot, do pacote spdep. O problema é que o gráfico não é “dos mais bacanas”. Uma demonstração gráfica do teste é feita com a comparação dos resíduos, defasados e não defasados, das regressões feitas acima, o que demonstraria heterocedasticidade dos modelos. De certa forma, esse é o teste feito na função lm.morantest de antes. Assim, vamos construir esse gráfico manualmente. O gráfico vai contrapor os resíduos das regressões condicionadas e a sua defasagem espacial (utilizando a função lag.listw).
No gráfico abaixo, mais uma vez para simplificação, foi usado somente uma das regressões, a “CC9110”.
ggplot(BASE) +
geom_point(aes(x = CC9110$residuals, y = lag.listw(WR1,CC9110$residuals)),
colour = "blue", alpha = 1/5) +
theme_light() +
geom_hline(aes(yintercept = 0), colour = "black") +
geom_vline(aes(xintercept = 0), colour = "black") +
geom_smooth(aes(x = CC9110$residuals,
y = lag.listw(WR1,CC9110$residuals)),
method = lm, fullrange = TRUE, colour = "blue") +
coord_cartesian(xlim = c(-1,1), ylim = c(-1,1)) +
labs( title = "Gráfico do Teste I de Moran",
x = "Resíduos da regressão",
y = "Resíduos defasados")
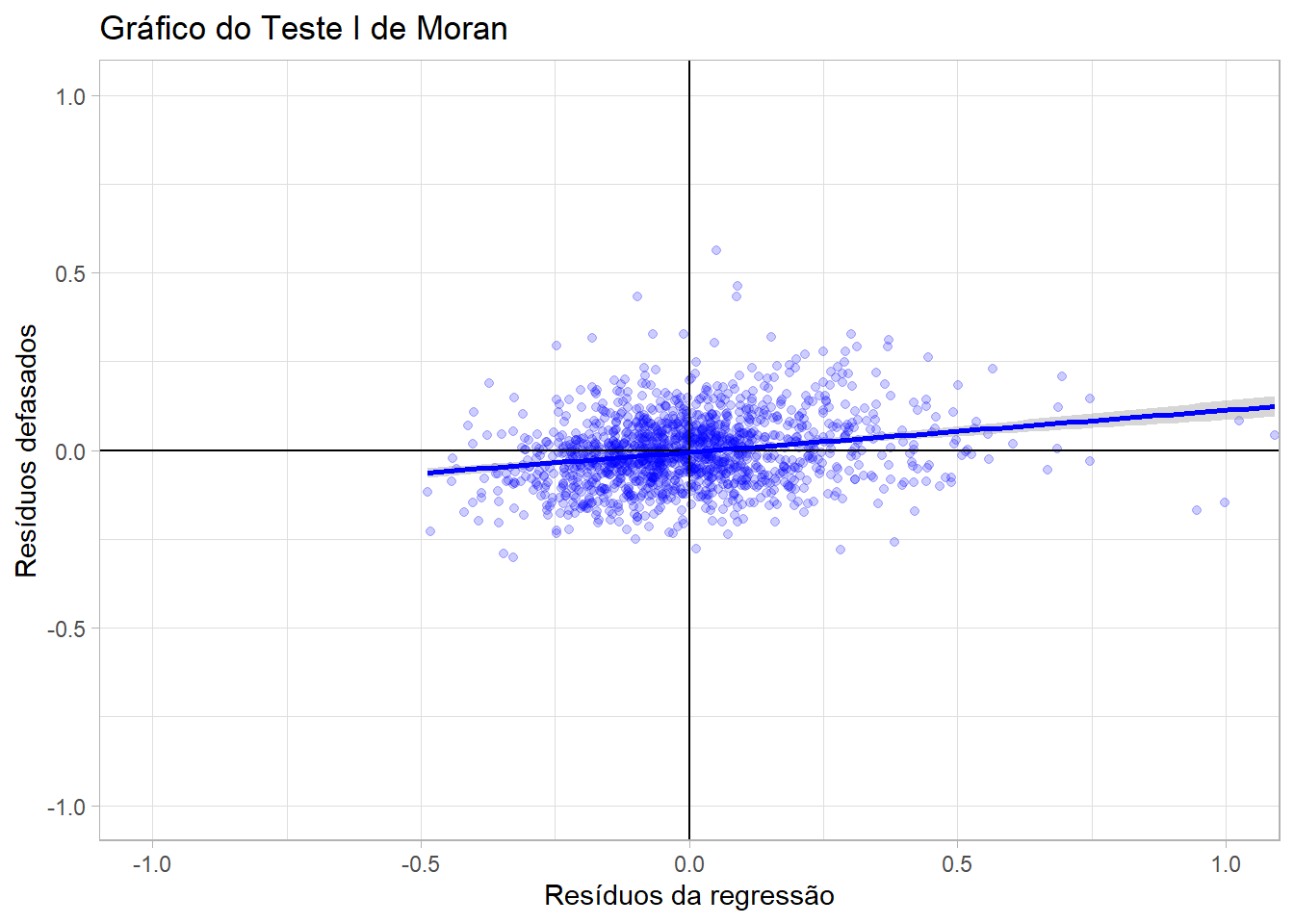
A presença da dependência espacial é evidenciada pela nuvem de pontos distantes do ponto central do gráfico (0,0) e pela linha de tendência traçada. Entretanto, este é um teste visual, a evidência estatística da dependência espacial deve ser confirmada pelo I de Moran.
Assim, foi identificado que, nos modelos que testamos, as regressões apresentavam dependência espacial em relação aos seus vizinhos. Ou seja, o crescimento da produtividade desses municípios era influência pelo crescimento da produtividade dos seus vizinhos.
O próximo texto sobre o artigo deve mostrar os diferentes modelos de aplicação. Particularmente essa série está um pouco mais longa do que gostaria, mas devo finalizá-la nos próximos dois textos, espero!
- Mais detalhes podem ser vistos em Carvalho Ywata e Albuquerque. [return]
