Apresentação
Estou prometendo disponibilizar os scripts para reprodução do artigo baseado em minha dissertação, mas tem sido complicado. Decidi que para conseguir cumprir esse objetivo terei que dividir a tarefa. Assim, serão três posts contando este. Os próximos apresentarão os testes para dependência espacial e os modelos e o último tratará dos efeitos espaciais comuns. Um resumo do que trata o artigo pode ser encontrado aqui.
Base de dados
Para fazer a dissertação e, consequentemente, o artigo, utilizei dados dos municípios nordestinos dos Censos de 1991, 2000 e 2010. Há um problema de se trabalhar com municípios que é que eles mudam ao longo do tempo. Há emancipações e até extinções. Uma sugestão de Reis et al., acatada na pesquisa, é de trabalhar com áreas mínimas comparáveis. Nesse sentido o que chamo de municípios são, na verdade, áreas mínimas comparáveis (AMC) do nordeste brasileiro. Para fazer isso com os dados do censo é necessário agregar municípios, o que dá algum trabalho. Neste momento não vou disponibilizar os procedimentos para ganhar em objetividade, talvez mais para frente. Assim, vou disponibilizar a base que utilizei. Para tanto coloquei ela no github. O arquivo conta com os códigos municípais com seis dígitos. As taxas de crescimento da produtividade, em logarítmo, para os diferentes períodos: 1991-2010, 1991-2000, 2000-2010. Também estão ali as produtividades em logaritmo dos anos de 1991 e 2000. Para essa variável foi considerado o salário médio do município, por hora trabalhada. Além disso estão disponíveis as variáveis de controle para os anos de 1991 e 2000. As variáveis de controle são Escolaridade, percentual da população com ensino médio completo, grau de urbanização, percentual de analfabetos na população, população em logaritmo, horas trabalhadas, salário e dummys para os estados. Não vou detalhar tudo, mas para maiores informações você pode olhar a dissertação, o artigo, ou deixar um comentário.
BASE <- read.csv("http://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/NE1991.csv", header = T)
stargazer(head(BASE), type = "html",
summary = F, align = T) #necessário carregar o pacote stargazer| X | MUN | lng9110 | lng9100 | lng0010 | lnProd1991 | lnProd2000 | lnProd2010 | Escol1991 | Escol2000 | EMedio1991 | EMedio2000 | Urb1991 | Urb2000 | Analf1991 | Analf2000 | Gini1991 | Gini2000 | LnPop1991 | LnPop2000 | Indus1991 | Indus2000 | Serv1991 | Serv2000 | Horas1991 | Horas2000 | Horas2010 | Sal1991 | Sal2000 | Sal2010 | MA | PI | CE | RN | PB | PE | AL | SE | BA | |
| 1 | 210,010 | 210,010 | 1.022 | 0.200 | 0.822 | 2.129 | 2.330 | 3.152 | 3.672 | 5.285 | 0.032 | 0.097 | 0.347 | 0.482 | 0.608 | 0.431 | 0.884 | 0.893 | 8.429 | 8.451 | 0.260 | 0.150 | 0.482 | 0.628 | 38.207 | 39.767 | 48.413 | 324.126 | 366.061 | 707.554 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 210,020 | 210,020 | 1.001 | 0.231 | 0.770 | 2.599 | 2.831 | 3.600 | 6.029 | 6.652 | 0.175 | 0.183 | 0.204 | 0.266 | 0.475 | 0.309 | 0.837 | 0.916 | 9.883 | 9.966 | 0.286 | 0.142 | 0.380 | 0.635 | 40.600 | 36.322 | 45.738 | 525.640 | 564.942 | 775.574 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 210,030 | 210,030 | 0.455 | 0.049 | 0.405 | 2.623 | 2.673 | 3.078 | 4.165 | 5.932 | 0.055 | 0.119 | 0.279 | 0.392 | 0.666 | 0.472 | 0.846 | 0.907 | 9.879 | 9.843 | 0.283 | 0.144 | 0.443 | 0.690 | 42.586 | 42.532 | 64.301 | 401.963 | 468.960 | 733.660 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 210,040 | 210,040 | 0.212 | -0.303 | 0.514 | 2.787 | 2.485 | 2.999 | 3.750 | 5.951 | 0.171 | 0.084 | 0.121 | 0.263 | 0.600 | 0.443 | 0.851 | 0.861 | 9.904 | 9.867 | 0.100 | 0.154 | 0.354 | 0.637 | 34.999 | 39.614 | 48.217 | 620.248 | 385.851 | 588.369 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 210,050 | 210,050 | 0.659 | 0.036 | 0.623 | 2.906 | 2.943 | 3.565 | 5.652 | 6.292 | 0.147 | 0.144 | 0.436 | 0.593 | 0.334 | 0.240 | 0.876 | 0.892 | 9.243 | 9.228 | 0.326 | 0.157 | 0.338 | 0.667 | 38.176 | 44.309 | 53.417 | 685.375 | 666.616 | 1,039.950 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 210,060 | 210,060 | 0.293 | -0.325 | 0.618 | 2.854 | 2.529 | 3.147 | 5.922 | 5.507 | 0.123 | 0.073 | 0.318 | 0.346 | 0.512 | 0.308 | 0.900 | 0.904 | 10.048 | 10.351 | 0.264 | 0.209 | 0.396 | 0.603 | 39.804 | 45.732 | 60.896 | 687.382 | 488.196 | 762.167 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Convergência Absoluta
A convergência absoluta é mais simples de identificar. Apenas com uma figura gráfica é possível saber se ela conteceu ou não.
library(ggplot2)
ggplot(BASE) +
geom_point(aes(x = lnProd1991,y = lng9110),
color = "blue", alpha = 1/3) +
geom_point(aes(x = lnProd1991, y = lng9100),
color = "red", alpha = 1/3) +
geom_point(aes(x = lnProd2000, y = lng0010),
color = "green", alpha = 1/3) +
labs(y = "Taxa de Crescimento", x = "Produtividade Inicial")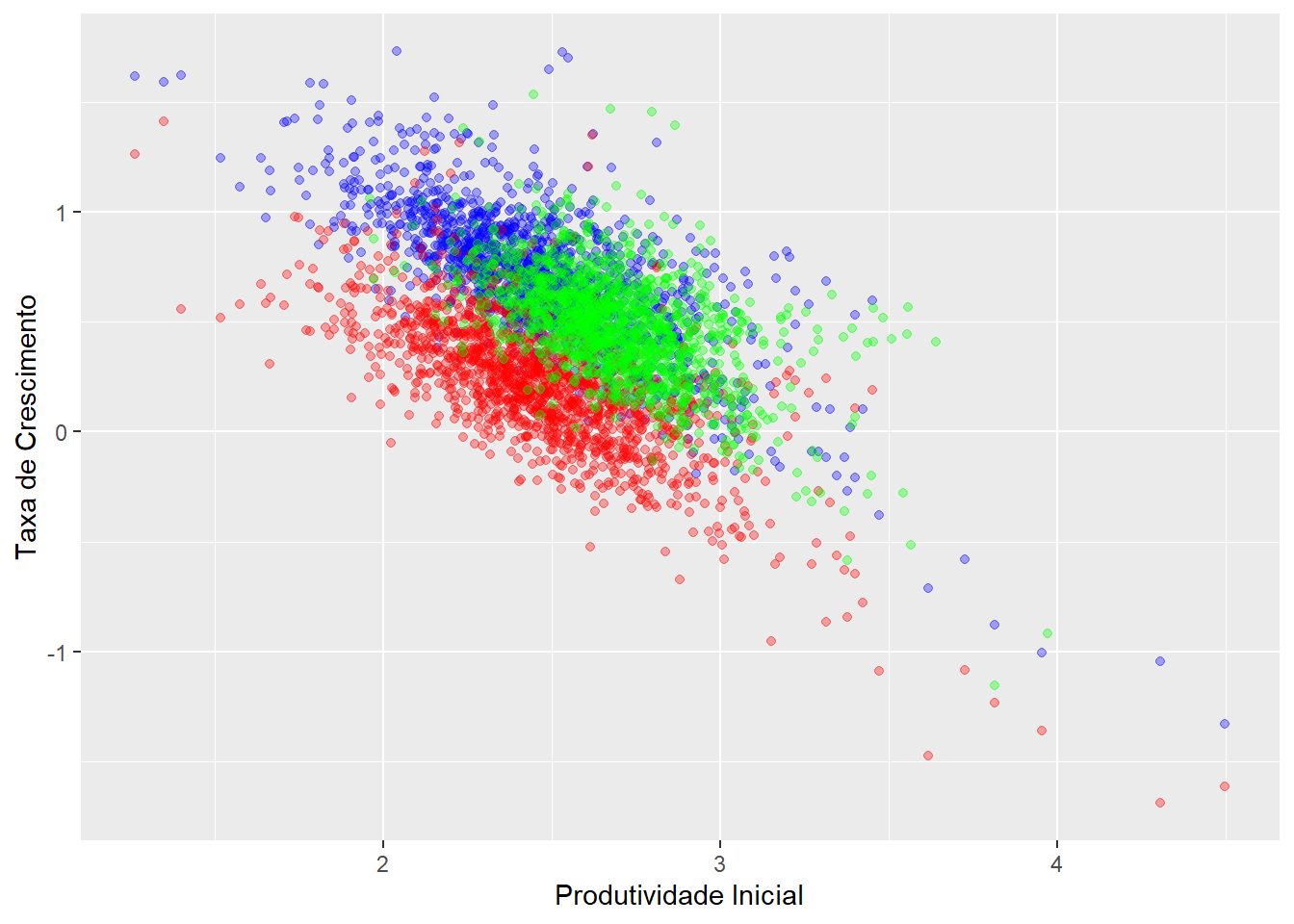
A inclinação negativa dos pontos sugere que houve convergência absoluta. Ou seja, os municípios mais pobres, com menor Produtividade Inicial, tiveram maiores taxas de crescimento no período.
Regressão
Convergência Absoluta
A regressão para convergência absoluta é uma regressão simples, tal que:
\[\log(Taxa de Crescimento Produtvidade) = \alpha + \beta Produtividade Inicial + \varepsilon\]
Para a estimação se utiliza o comando lm de linear model (regressão linear).
CA9110<-lm(lng9110~lnProd1991, data=BASE)
CA9100<-lm(lng9100~lnProd1991, data=BASE)
CA0010<-lm(lng0010~lnProd2000, data=BASE)
stargazer(CA9110, CA9100, CA0010, type = "html")| Dependent variable: | |||
| lng9110 | lng9100 | lng0010 | |
| (1) | (2) | (3) | |
| lnProd1991 | -0.749*** | -0.704*** | |
| (0.018) | (0.018) | ||
| lnProd2000 | -0.596*** | ||
| (0.023) | |||
| Constant | 2.550*** | 1.956*** | 2.084*** |
| (0.044) | (0.045) | (0.062) | |
| Observations | 1,451 | 1,451 | 1,451 |
| R2 | 0.553 | 0.517 | 0.315 |
| Adjusted R2 | 0.553 | 0.516 | 0.314 |
| Residual Std. Error (df = 1449) | 0.209 | 0.211 | 0.203 |
| F Statistic (df = 1; 1449) | 1,794.525*** | 1,549.752*** | 665.363*** |
| Note: | p<0.1; p<0.05; p<0.01 | ||
Mais uma vez, para ganhar em objetividade, não estou organizando as tabelas, só replicando os resultados. Para ser sincero, na dissertação e no artigo utilizei o Excel mesmo. Hoje já tenho um pouco mais de know-how no R, mas ainda não parei para olhar tabelas. Assim fica para uma próxima também.
Convergência Condicionada
A covnergência condicionada, como o nome sugere, condiciona a regressão as variáveis de controle. A ideia é filtrar variações que possam ser causadas por outras motivações. Como por exemplo tamanho da população, escolaridade, estrutura produtiva. Tudo isso afeta a variável renda de alguma forma e as diferentes composições devem influenciar diferentemente nas taxas de crescimento. O modelo é semelhante:
\[ \log(Taxa de Crescimento Produtvidade) = \alpha + \beta_0 Produtividade Inicial + \beta_iControles + \varepsilon \]
E as regressões também são análogas:
CC9110 <- lm(lng9110~lnProd1991+EMedio1991+Analf1991
+Urb1991+LnPop1991+Indus1991+Serv1991+Gini1991, data=BASE)
CC9100 <- lm(lng9100~lnProd1991+EMedio1991+Analf1991
+Urb1991+LnPop1991+Indus1991+Serv1991+Gini1991, data=BASE)
CC0010 <- lm(lng0010~lnProd2000+EMedio2000+Analf2000
+Urb2000+LnPop2000+Indus2000+Serv2000+Gini2000, data=BASE)
stargazer(CC9110, CC9100, CC0010, type = "html")| Dependent variable: | |||
| lng9110 | lng9100 | lng0010 | |
| (1) | (2) | (3) | |
| lnProd1991 | -0.871*** | -0.807*** | |
| (0.018) | (0.019) | ||
| EMedio1991 | 0.340*** | 0.547*** | |
| (0.130) | (0.137) | ||
| Analf1991 | -0.286*** | -0.266*** | |
| (0.069) | (0.073) | ||
| Urb1991 | 0.184*** | 0.109*** | |
| (0.031) | (0.032) | ||
| LnPop1991 | 0.061*** | 0.038*** | |
| (0.006) | (0.007) | ||
| Indus1991 | -0.236*** | -0.264*** | |
| (0.061) | (0.064) | ||
| Serv1991 | -0.015 | -0.003 | |
| (0.077) | (0.082) | ||
| Gini1991 | -0.468** | -0.278 | |
| (0.213) | (0.225) | ||
| lnProd2000 | -0.748*** | ||
| (0.024) | |||
| EMedio2000 | 0.069 | ||
| (0.114) | |||
| Analf2000 | -0.373*** | ||
| (0.079) | |||
| Urb2000 | 0.108*** | ||
| (0.030) | |||
| LnPop2000 | 0.065*** | ||
| (0.006) | |||
| Indus2000 | 0.213** | ||
| (0.100) | |||
| Serv2000 | 0.213*** | ||
| (0.066) | |||
| Gini2000 | -0.961*** | ||
| (0.200) | |||
| Constant | 2.753*** | 2.170*** | 2.605*** |
| (0.199) | (0.210) | (0.170) | |
| Observations | 1,451 | 1,451 | 1,451 |
| R2 | 0.640 | 0.576 | 0.444 |
| Adjusted R2 | 0.638 | 0.574 | 0.441 |
| Residual Std. Error (df = 1442) | 0.188 | 0.199 | 0.183 |
| F Statistic (df = 8; 1442) | 320.733*** | 245.050*** | 144.107*** |
| Note: | p<0.1; p<0.05; p<0.01 | ||
Por fim, achei um pacote no R para expor os resultados dos coeficientes com seus respectivos erros-padrão. Serve só uma visualização diferente dos resultados.
library(dotwhisker)
dwplot(list(CC9110, CC9100, CC0010))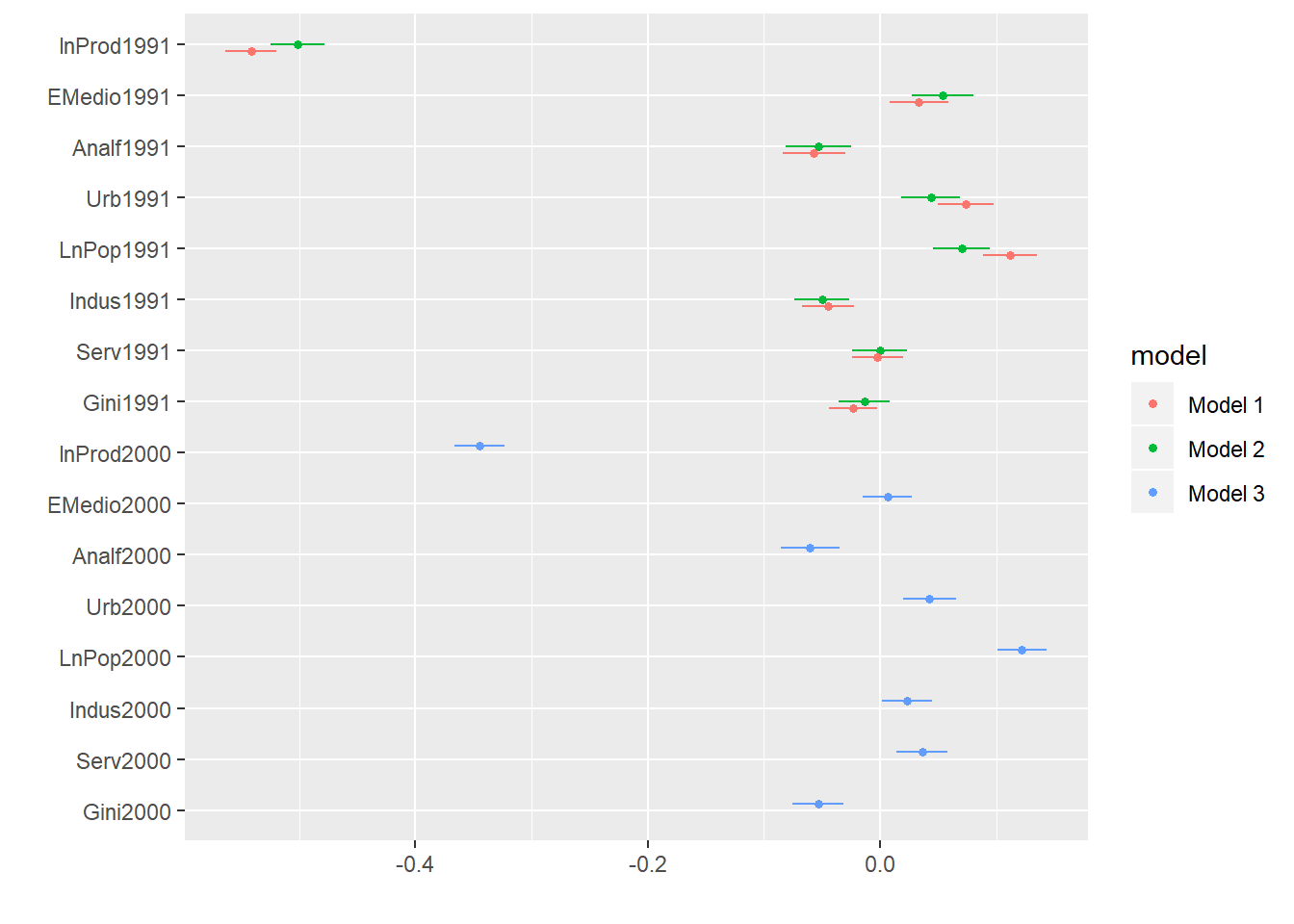
Comentários finais
Pois bem, está um pouco superficial. Não estou comentando os resultados, pois o objetivo aqui é disponibilizar os scripts para reprodução. Nem detalhei muito os comandos ou arrumei as tabelas de resultados, mas isso era para concluir outro objetivo deste post: começar a publicar essa série de uma vez!! Caso queira mais detalhes, pergunte nos comentários. Para as próximas postagens tentarei ser mais detalhista.
