Este texto finaliza a série de textos que objetivava a reprodução dos resultados do artigo publicado, baseado em minha dissertação de mestrado. Entretanto,este texto não faz parte, nem da dissertação, nem do artigo. É um complemento que faço como sugestão para melhorar a apresentação dos resultados.
Links úteis
Como aqui só apresentarei os resultados, sem muita discussão, seguem os links do que já foi apresentado.
Dissertação que originou o artigo, aqui;
Artigo publicado, aqui;
Resumo do que trata o artigo, aqui;
Reprodução das análises de convergência absoluta e condicionada,aqui;
Neste texto, é apresentado e aplicado o teste para identificar a dependência espacial no modelo;
Aqui, foram feitos os testes para identificar a modelagem mais adequado;
Este texto traz as regressões dos modelos espacializados;
Neste, estão os procedimentos para as regressões em painel.
Pacotes
O foco deste texto é a representação dos resultados de forma gráfica. Assim, será necessário gerar novamente as regressões, tabelar os resultados para, enfim, gerar os gráficos. Com isso, os seguintes pacotes são necessários:
library(spdep)
library(plm)
library(splm)
library(spatialreg)
library(ggplot2)
library(tidyverse)
library(stringr)Base de dados
A base de dados se mantém a mesma utilizada nos outros textos, e soma-se às transformações necessárias para o painel, feitas no último texto.
#Leitura da Base de Dados
BASE <- read.csv("http://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/NE1991.csv"
, header = T)
#Leitura da matriz de vizinhança
R1<-read.gal("https://raw.githubusercontent.com/RodrigoAnderle/Artigos-Reproduz-veis/master/Fatores%20Espaciais%20Comuns%20(RBERU)/R1.gal"
,BASE$MUN)
WR1<-nb2listw(R1) # ajuste necessário para utilização nas funções
# Transformando base em painel
SB1991 <-BASE[,c(2,4,6,9,11,13,15,17,19,21,23,31:39)]
SB1991$ANO <- 1991
colnames(SB1991)<- c("MUN","TAXA","PRODUT","ESCOL","EMED","URB",
"ANALF","GINI","LNPOP","INDUS","SERV",
"MA","PI","CE","RN","PB","PE","AL","SE","BA",
"ANO")
SB2000 <- BASE[,c(2,5,7,10,12,14,16,18,20,22,24,31:39)]
SB2000$ANO <- 2000
colnames(SB2000)<- c("MUN","TAXA","PRODUT","ESCOL","EMED","URB",
"ANALF","GINI","LNPOP","INDUS","SERV",
"MA","PI","CE","RN","PB","PE","AL","SE","BA",
"ANO")
BASE2 <- rbind(SB1991,SB2000)
BASE2 <- pdata.frame(BASE2, index = c("MUN", "ANO"))
### Inserindo defasagem espacial nas explicativas
BASE2$W_PRODUT <- slag(BASE2$PRODUT,WR1)
BASE2$W_ESCOL <- slag(BASE2$ESCOL,WR1)
BASE2$W_EMED <- slag(BASE2$EMED,WR1)
BASE2$W_URB <- slag(BASE2$URB,WR1)
BASE2$W_ANALF <- slag(BASE2$ANALF,WR1)
BASE2$W_GINI <- slag(BASE2$GINI,WR1)
BASE2$W_LNPOP <- slag(BASE2$LNPOP,WR1)
BASE2$W_INDUS <- slag(BASE2$INDUS,WR1)
BASE2$W_SERV <- slag(BASE2$SERV,WR1)Regressões
As mesmas regressões, descritas nos outros textos, serão replicadas.
# Modelo com defasagem espacial sacsar
CC9110S<-sacsarlm(lng9110~lnProd1991+EMedio1991+Analf1991+Urb1991
+LnPop1991+Indus1991+Serv1991+Gini1991,
data = BASE,
listw = WR1)
#Durbin Espacial
CC9110DS<-sacsarlm(lng9110 ~ lnProd1991 + EMedio1991 + Analf1991 +Urb1991
+LnPop1991+Indus1991+Serv1991+Gini1991,
data = BASE,
listw = WR1,
type="sacmixed")
# Painel de Efeitos fixos SARMA espacial
plm_PIB<- spml(TAXA ~ PRODUT + EMED + ANALF + URB + LNPOP + INDUS +
SERV + GINI,data = BASE2, listw = WR1, listw2 = WR1,
model = "within",lag = T, effect = "twoways",
spatial.error = "kkp")
# Painel de Efeitos Fixos Durbin Espacial
DSplm_PIB<- spml(TAXA ~ PRODUT + EMED + ANALF + URB + LNPOP + INDUS +
SERV + GINI + W_PRODUT + W_EMED + W_ANALF + W_URB +
W_LNPOP + W_INDUS + W_SERV + W_GINI + W_PRODUT
,data = BASE2, listw = WR1, listw2 = WR1,
model = "within",lag = T, effect = "twoways",
spatial.error = "kkp")Tabelando resultados das regressões
A ideia é inserir os diferentes resultados dos modelos anteriores em uma tabela só, tornando mais fácil a produção dos gráficos. Além dos coeficientes, estou inserindo uma coluna para cada intervalo de confiança - que, para simplificação, estão sendo considerados como simétricos - outra coluna para o nome das variáveis e outra que cumpre o papel de uma dummy, indicando se a variável se trata da variável em si, ou de sua defasagem espacial. Na representação gráfica isso fará mais sentido.
# Coeficientes e intervalor de confiança
CCS9110 <- data.frame(Coeficiente = coefficients(CC9110S),
ci.lb=confint(CC9110S)[,1],
ci.ub=confint(CC9110S)[,2],
Modelo = "CCS9110")
#Inserindo coluna de variáveis
CCS9110$Variáveis <- c("rho", "lambda", "Constante", "Produtividade (Ln)",
"Ensino Médio", "Analfabetos", "Urbanização",
"População (Ln)", "Indústria", "Serviços", "Gini")
#Inserindo dummy para difrenciar defasagens
CCS9110$Lag <- rep("Variáveis",11)
# Coeficientes e intervalor de confiança
CCDS9110 <- data.frame(Coeficiente = coefficients(CC9110DS),
ci.lb = confint(CC9110DS)[,1],
ci.ub = confint(CC9110DS)[,2],
Modelo = "CCDS9110")
#Inserindo coluna de variáveis
CCDS9110$Variáveis <- c("rho", "lambda", "Constante", "Produtividade (Ln)",
"Ensino Médio", "Analfabetos", "Urbanização",
"População (Ln)", "Indústria", "Serviços", "Gini",
"Produtividade (Ln)",
"Ensino Médio", "Analfabetos", "Urbanização",
"População (Ln)", "Indústria", "Serviços",
"Gini")
#Inserindo dummy para difrenciar defasagens
CCDS9110$Lag <- c(rep("Variáveis",11), rep("Defasagem Espacial",8))
# Coeficientes e intervalor de confiança
PCCS9110 <- data.frame(Coeficiente = coefficients(plm_PIB),
ci.lb = coefficients(plm_PIB) - 1.96*sqrt(diag(plm_PIB$vcov)),
ci.ub = coefficients(plm_PIB) + 1.96*sqrt(diag(plm_PIB$vcov)),
Modelo = "PCCS9110")
#Inserindo coluna de variáveis
PCCS9110$Variáveis <- c("rho", "lambda", "Produtividade (Ln)",
"Ensino Médio", "Analfabetos", "Urbanização",
"População (Ln)", "Indústria", "Serviços", "Gini")
#Inserindo dummy para difrenciar defasagens
PCCS9110$Lag <- rep("Variáveis",10)
# Coeficientes e intervalor de confiança
PCCDS9110 <- data.frame(Coeficiente = coefficients(DSplm_PIB),
ci.lb = coefficients(DSplm_PIB) - 1.96*sqrt(diag(DSplm_PIB$vcov)),
ci.ub = coefficients(DSplm_PIB) + 1.96*sqrt(diag(DSplm_PIB$vcov)),
Modelo = "PCCDS9110"
)
#Inserindo coluna de variáveis
PCCDS9110$Variáveis <- c("rho", "lambda","Produtividade (Ln)",
"Ensino Médio", "Analfabetos", "Urbanização",
"População (Ln)", "Indústria", "Serviços", "Gini",
"Produtividade (Ln)",
"Ensino Médio", "Analfabetos", "Urbanização",
"População (Ln)", "Indústria", "Serviços",
"Gini")
#Inserindo dummy para difrenciar defasagens
PCCDS9110$Lag <- c(rep("Variáveis",10), rep("Defasagem Espacial",8))
# Colocando tudo em uma base só!
TABELA <- rbind(CCS9110,CCDS9110,PCCS9110,PCCDS9110)Ordenando variáveis
Para uma melhor representação é importante que as informações sigam uma determinada ordem. As variáveis que são compostas por palavras precisam ser tratadas como factors e reordenadas, do contrário, vão aparecer em ordem alfabética. Isso é feito no procedimento abaixo:
TABELA$Variáveis <- factor(TABELA$Variáveis,
levels = c("Gini", "Serviços","Indústria","População (Ln)","Urbanização",
"Analfabetos","Ensino Médio","Produtividade","Constante",
"lambda", "rho"))
TABELA$Lag <- factor(TABELA$Lag, levels = c("Variáveis","Defasagem Espacial"))
TABELA$Modelo <- factor(TABELA$Modelo,
levels = c("CCS9110", "PCCS9110", "CCDS9110", "PCCDS9110"))Apresentando Resultados
Tentei utilizar o dotwhisker, mas ele não funcionou nos modelos sarml. Pesquisando um pouco mais, encontrei esta descrição que reproduz gráficos parecidos. Os resultados são apresentados a seguir.
Impacto da Vizinhança no crescimento
O primeiro resultado que vou apresentar diz respeito a um dos focos da dissertação e do artigo, o impacto do crescimento dos vizinhos no crescimento de um município nordestino. Como expliquei aqui, em um trabalho de referência, esse resultado era negativo.
Para simplificação, só estou apresentando os resultados para o período entre 1991 e 2010, em cross-section, e de 1991,2000 e 2010, para o painel, com as defasagens na variável dependente, “rho”, e no termo de erro, “lambda” presentes nos modelos SARMA e Durbin Spatial.
Fica claro que o modelo em painel já “resolve” essa questão, pois considera os efeitos fixos de cada município, demonstrando que o crescimento da vizinhança não impacta negativamente no crescimento. Na dissertação, isso foi resolvido com o modelo Durbin Spatial (DS), pois só utilizei dados cross-section. Desconfio que um painel só com três períodos (1991,2000,2010) pode apresentar problemas, mas não aprofundei a questão.
De toda forma, o objetivo era evidenciar que haviam particularidades regionais que, quando desconsideradas, levavam à conclusão de que os municípios eram impactados negativamente pelo crescimento dos seus vizinhos.
TABELA %>%
filter(Variáveis == "rho" | Variáveis == "lambda") %>%
ggplot(aes(x = Coeficiente, y = Variáveis, colour = Modelo)) +
geom_point(size = 2, show.legend = F) +
geom_segment(show.legend = F,size = 1,
aes(x = ci.lb, xend = ci.ub, y = Variáveis, yend = Variáveis)) +
theme_light() +
geom_vline(xintercept = 0, size = 1 , show.legend = F ) +
facet_wrap(vars(Modelo)) +
labs(x = NULL, y = NULL,
title = "Coeficientes das Defasagens Espaciais",
subtitle = "Modelos de crescimento da produtividade para municípios Nordestinos",
caption = "Notas:
rho: Defasagem espacial do crescimento da produtividade;
lambda: Defasagem espacial do termo de erro;
CCS9110: Modelo de Convergência Condicionada de 1991 a 2010;
CCDS9110: Mesmo modelo com aplicação de defasagem espacial nas variáveis;
PCC9110: Modelo de Convergência Condicionada em Painel(1991,2000,2010);
PCCDS9110: Mesmo modelo que o anterior com defasagem espacial nas variáveis.") 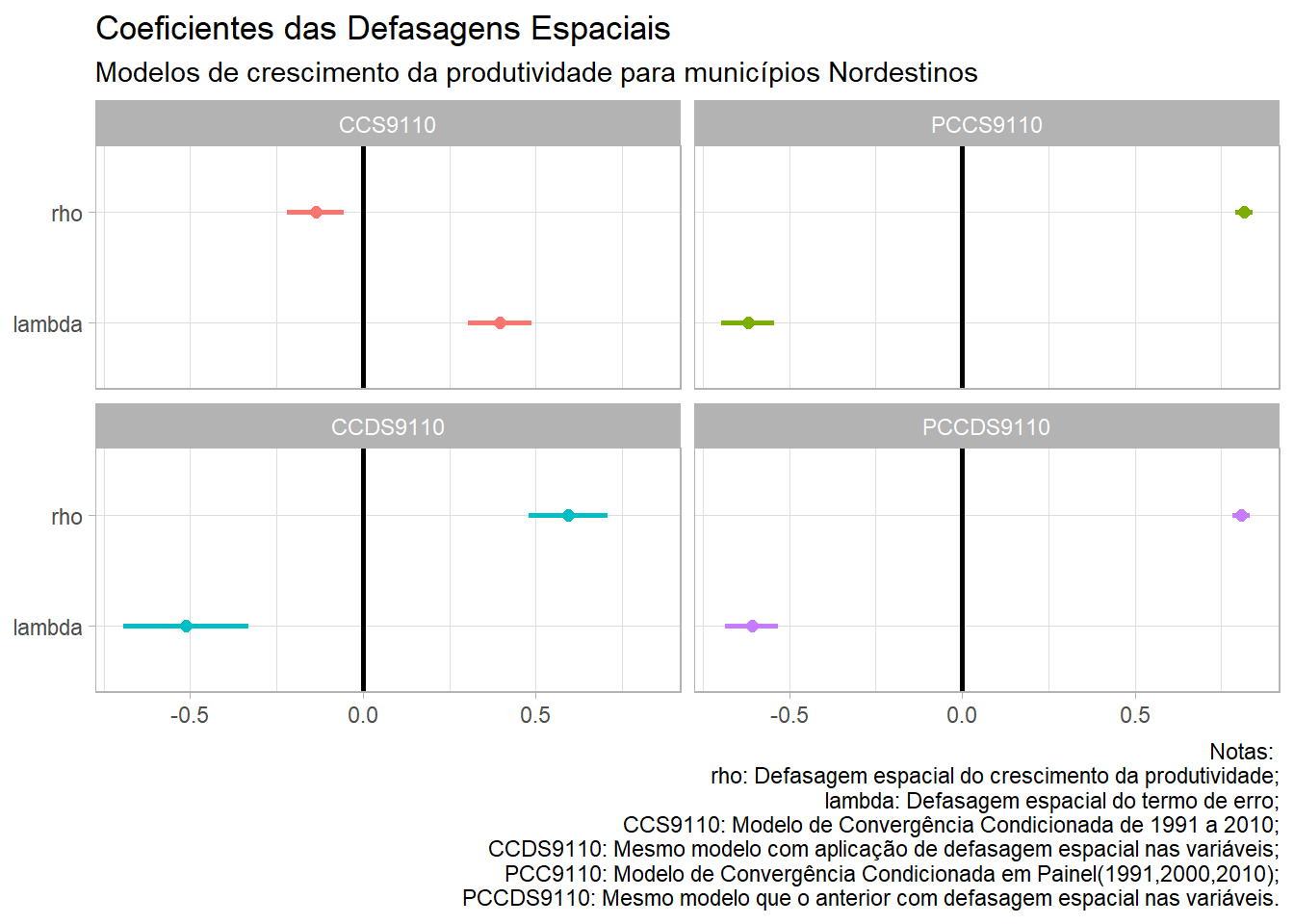
Note que a produção do gráfico utiliza os pacotes ggplot2e tidyverse.
Neste primeiro gráfico, são filtrados os resultados para os termos “rho” e “lambda”, definindo o eixo “x” para os coeficientes e o “y” para as variáveis, separando os modelos por cor (colour). Em seguida, é inserido o gráfico de pontos (geom_point) e o segmento de reta para simbolizar o intervalor de confiança (geom_segment). Além disso, inseri uma linha para ressaltar o zero (geom_vline) e dividi os gráficos por modelos (facet_wrap).
Adicionei uma série de “perfumarias” com o labs, que não tive paciência de manter nos outros gráficos, e utilizei o theme_light() para um gráfico mais limpo.
Variáveis de controle
Em seguida, apresento os resultados para as variáveis de controle. Tanto na dissertação, quanto no artigo, estes resultados eram mais interessantes quando comparados entre os diferentes recortes: 1991-2010,1991-2000,2000-2010. Aqui, entretanto, meu objetivo é ilustrar como apresentar os resultados. Portanto, não farei todas essas representações.
O primeiro gráfico apresenta os resultados dos modelos sem o SARMA, comparando os resultados do cross-section com o do painel. Claramente, o segundo tem uma diminuição no termo de erro dos coeficientes.
O segundo gráfico apresenta os resultados para os modelos com o Durbin Spatial. Ou seja, apresenta as variáveis de controle e suas defasagens espaciais. Tanto no artigo, quanto na dissertação, destaquei um comportamento de concorrência entre as variáveis e suas defasagens espaciais, mas isso não fica claro nestas representações, a não ser pela variável do coeficiente de gini. Isso era mais perceptível nos cortes entre 1991-2000 e 2000-2010.
Regressões sem Durbin Espacial
Diferente do primeiro gráfico, este filtra os modelos de interesse e exclui as variáveis “rho” e “lambda”.
O restante é bastante semelhante, só não dividi o gráfico e mantive a exclusão dos nomes nos eixos (labs(x = NULL, y = NULL).
TABELA %>%
filter(Modelo == "CCS9110" | Modelo == "PCCS9110") %>%
filter(Variáveis != "<NA>" & Variáveis != "rho" &
Variáveis != "lambda") %>%
ggplot(aes(x = Coeficiente, y = Variáveis, colour = Modelo)) +
geom_point(size = 2) +
geom_segment(show.legend = F,size = 1,
aes(x = ci.lb, xend = ci.ub, y = Variáveis, yend = Variáveis)) +
theme_light() +
geom_vline(xintercept = 0, size = 1 , show.legend = F ) +
labs(x = NULL, y = NULL)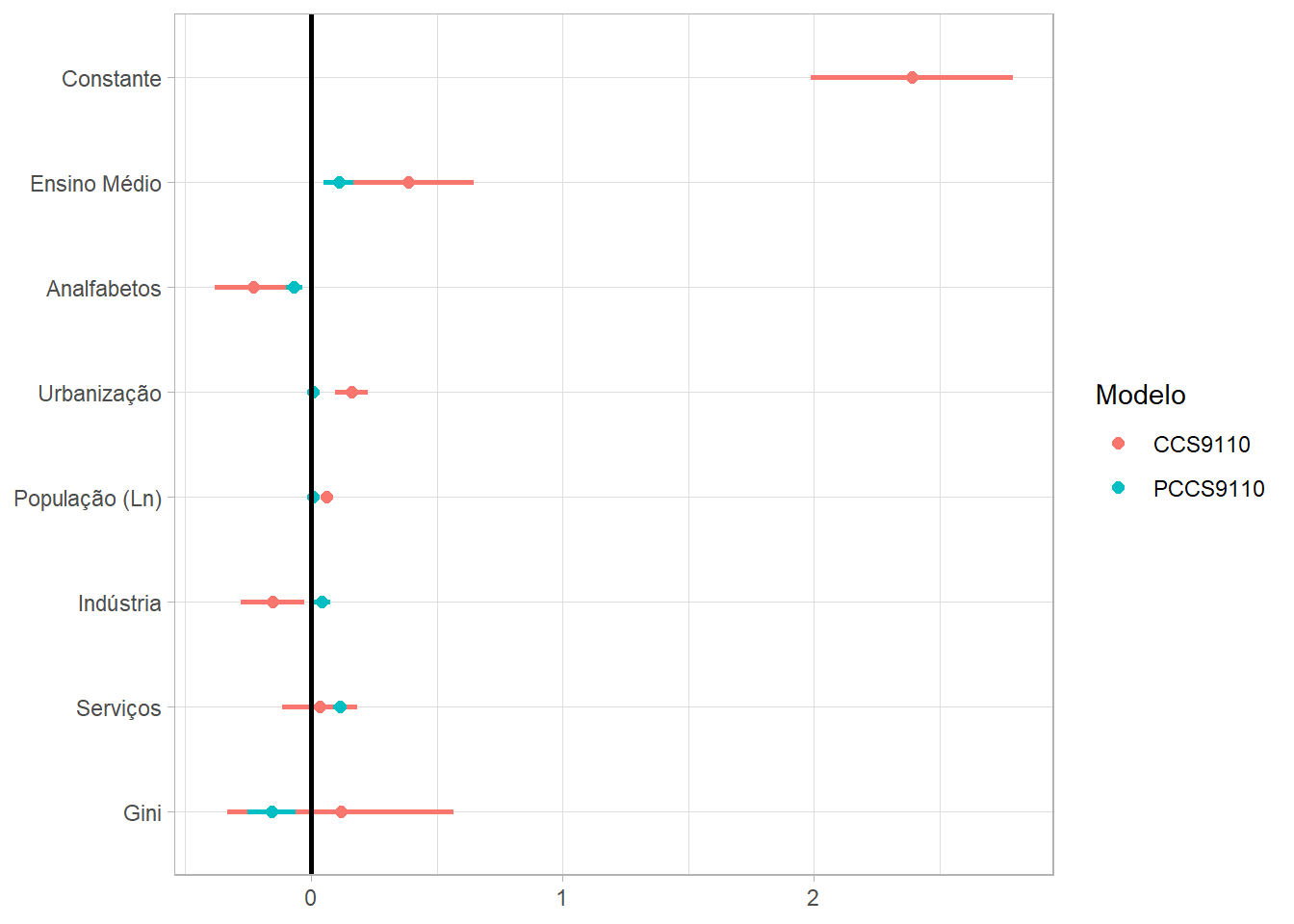
Regressões com Durbin Espacial
Este gráfico segue a mesma formatação, porém alterando os modelos de interesse e inserindo uma divisão do gráfico entre Variáveis e suas defasagens (facet_grid).
TABELA %>%
filter(Modelo == "CCDS9110" | Modelo == "PCCDS9110") %>%
filter(Variáveis != "<NA>", Variáveis != "rho",
Variáveis != "lambda") %>%
ggplot(aes(x = Coeficiente, y = Variáveis, colour = Modelo)) +
geom_point() +
geom_segment(show.legend = F,size = 1,
aes(x = ci.lb, xend = ci.ub, y = Variáveis, yend = Variáveis)) +
theme_light() +
geom_vline(xintercept = 0, size = 1 , show.legend = F ) +
facet_grid(cols = vars(Lag)) +
labs(x = NULL, y = NULL)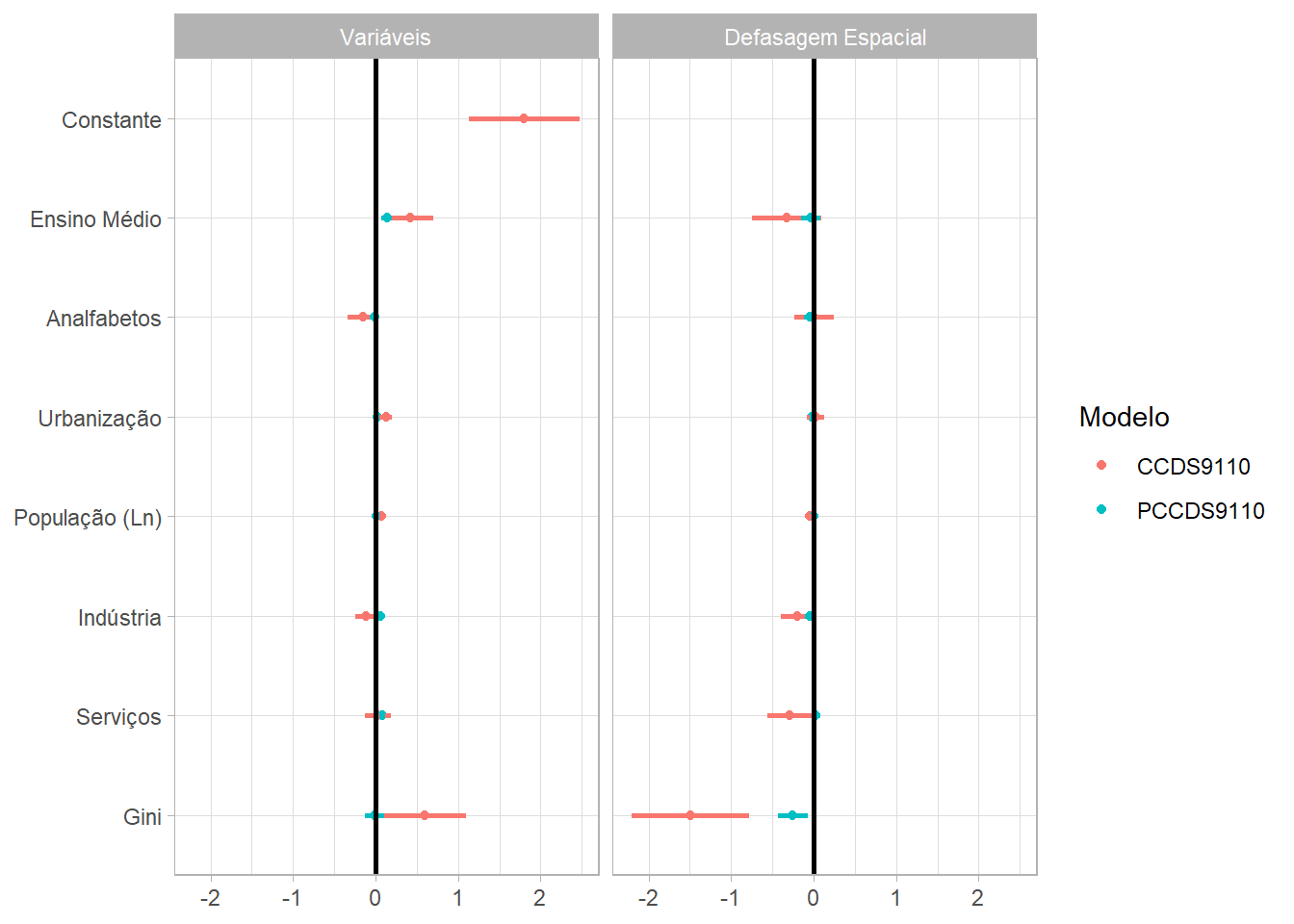
Finalizando
Aqui encerro a reprodução dos dados utilizados na minha dissertação e no artigo resultante dela. Mais uma vez, ressalto que não é nenhuma invenção da roda, mas é uma aplicação de método e tem seu valor acadêmico.
Este texto apresentou um item adicional, não havia utilizado este tipo de representação na dissertação, nem no artigo. Note que, em geral, os resultados do modelo de painel com efeitos fixos apresentaram menor variância (sugerida pelo intervalo de confiança reduzido) e variáveis de controle com coeficientes muito próximo de zero. Estes resultados não foram explorados no artigo, nem na dissertação e ficaram mais evidentes nesta representação. Isto demonstra a importância desse tipo de representação, algo que ficou faltando no estudo.
Para quem tiver interesse, além desses textos, tanto a dissertação, quanto o artigo, possuem uma série de referências para aplicações do genêro.
